The Complex SAT Math Problem Even the College Board Got Wrong

From Popular Mechanics

You can probably distill high school down into a few singularly agonizing days, but none shook you to the core quite like that one Saturday morning in junior year when you took the SATs.

If you’re like us, the memories are still painfully vivid, from the grating smell of freshly sharpened No. 2 pencils, to the burden of sitting still for hours with a bursting bladder, to the creeping click of the ticking clock counting down the minutes until the end of the exam and the beginning of the rest of your life. Clearly, we’re still working some things out.

And from what the teens tell us, the current SAT experience remains as harrowing as ever, virtually unchanged save for one new, particularly savage wrinkle: Now you might get some test answers wrong, even when you actually get them right.

That was the case for as many as 50,000 high school students across the country, who earlier this year had their test scores raised when a sharp-eyed student and tutor disputed a question on the May 2019 SAT and successfully lobbied the College Board, the organization that administers the test, to officially change the accepted answer.

As Compass Education Group points out, the offending question appeared near the very end of the marathon exam, in the final 55-minute math portion that allowed students to use calculators. Here it is, exactly how it was printed on the test.

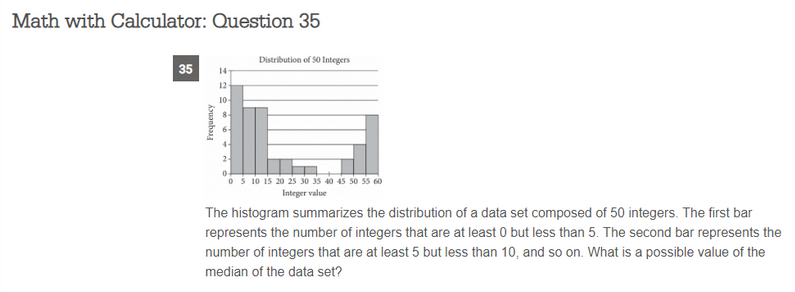
The question reads, “The histogram summarizes the distribution of a data set composed of 50 integers. The first bar represents the number of integers that are at least 0 but less than 5. The second bar represents the number of integers that are at least 5 but less than 10, and so on. What is a possible value of the median of the data set?”

Before you read on, can you figure it out?

We emphasized possible in italics because on this free-response portion of the SAT, students only had to provide “*a* correct answer,” as Compass’ Executive Director Bruce Reed writes on his blog, and thus, “the test makers must then account for every possible correct answer when scoring the test.”

“And that,” Reed writes, “is where the mistake was made.”

For starters, this is a pretty tricky problem because it’s presented as a histogram, which “can be nice for large data visualization,” says David Linkletter, “but awkward for specific little questions about points of data, as this problem illustrated.”

Linkletter is a Pure Mathematics Ph.D. candidate at the University of Nevada, Las Vegas whose research is in Set Theory - Large Cardinals. But, more crucially, he’s also a veteran SAT tutor, so he knows exactly what kinds of math problems make students tick the most.

In this histogram, Linkletter says, it isn’t clear if the boundary values belong to one bar or another, “so we get half of the question’s text just clarifying what numbers are supposed to be in each bar. Terrible aesthetics for a math question.”

Indeed, the presentation made the problem uglier, but it didn’t actually cause the error with the answer key. On the Compass blog, Reed talks through how to go about answering median problems.

To make sure we understood the question correctly, we threw it to Linkletter, a friend of Popular Mechanics who breaks down complex topics like the PEMDAS Paradox—applicable to the recent viral math problem that drove our entire staff insane—and asked him to weigh in.

“Math-minded kids love to mention that medians can end in .5,” Linkletter says. “Half the time I expect that to be part of the difficulty of the problem.”

While Linkletter says he would have happily answered 10.5—the lowest possible answer that uses the .5.—the veteran SAT tutor would’ve recommended his students write “12, 13, or something in the middle not playing with the .5 possibility, just to be safe.”

“But that’s supposed to be safety against your own misreading,” Linkletter says, “not against [the] College Board forgetting how medians work.”

When the College Board released the full answers to the May 2019 SAT a few weeks after the test, it only listed five correct integer values as the right answers to the question: 10, 11, 12, 13, and 14.

Like Linkletter, that didn’t sit right for one student who answered 12.5 and was insistent, along with their Compass tutor, that their response was also correct. So the student’s tutor wrote the following email to Compass HQ, wondering what gave:

Indeed, after Reed received the tutor’s question, he was also perplexed as to why 12.5 wasn’t an acceptable answer. So he reached out to the College Board for clarification. To Reed’s surprise, the College Board quickly copped to its mistake and ultimately raised the scores for those students who previously got the answer wrong. In some cases, “one raw score point can translate to 20-30 scaled points,” Reed writes. That’s not insignificant.

It’s unclear, exactly, just how many students were affected by the error. For his part, Reed thinks it’s probably somewhere between 25,000 and 50,000 students. But regardless of how many kids had their fortunes changed because of the blunder, this is a great example of why you should always stick to your convictions if you know have the numbers to show you’re right—even when everyone else says you’re wrong.

And hey, the College Board has made millions of students sweat for decades. It’s nice to return the favor for a change.

You Might Also Like

• This Device Can Send Messages Without Cell Service

• The Best Portable BBQ Grills for Cooking Anywhere

• The Best Video Game the Year You Were Born