Coronavirus: there's no one perfect model of the disease

The world is gripped by the COVID-19 pandemic, caused by the spread of a virus called SARS-CoV-2. Since the emergence of this new virus, mathematical modelling has been at the forefront of policy decision-making around the disease.
Mathematical modelling has already been used widely to help make decisions around the control of the COVID-19 spread. For example, the imposed social-distancing measures in the UK have been widely attributed to the projected outcomes of the COVID-19 epidemic based on a mathematical model led by Neil Ferguson’s research group at Imperial College London.
Models represent the spread of the virus as a graph with a curved line indicating how many infections there will probably be at any point in time. As the virus spreads, the line curves up until it peaks, and then falls down again as the virus is expected to eventually decline. The Imperial model suggests that the virus is still in the initial, fast-growing part of the epidemic curve.
More recently, another model, developed by the research group of Sunetra Gupta at Oxford University, suggested that “ongoing epidemics in the UK … started at least a month before the first reported death” and that the virus has already spread widely across the UK population.
Imperial v Oxford: which model is correct?
Do these seemingly differing findings mean that one model is more accurate than the other? And if so, which one is correct?
In truth, both models are mathematically sound and elegantly answer their posed questions using appropriate data. So more importantly than “which one is correct?”, we need to understand the differences between them and discuss why they come to seemingly different conclusions.
There are three main differences between the Imperial and the Oxford models. One, they use different modelling approaches. Two, they use different key parameters. And three, they pose and answer different questions.
Read more: How to model a pandemic
First, the Imperial model is a more complicated mathematical model that tracks the behaviour of each individual in the population and is hence called an “individual-based model”. It considers the infectiousness of each person in the population.
In contrast, the Oxford model is a mathematically simpler model that tracks the behaviour of different groups of people or “populations” and is therefore called a “population-based model”.
The populations tracked in time are those susceptible (S) to the virus, those infected by the virus (I) and those that recovered from the infection with the virus (R). This SIR model averages the infectiousness across the population.
In a limit case – that is, under certain model conditions – both models should come to the same conclusions. The fact that they don’t, is possibly due to points two and three, that is they use different key parameters and they pose and answer different questions.
Different parameters
Let’s look at the parameters first. We have heard a lot recently about two parameters associated with COVID-19: R0 and case fatality ratio. R0 (pronounced R nought) is what’s known as “the basic reproduction number”. It counts the number of people one person infected with the virus is likely to infect, on average. The latter is the case fatality ratio (CFR), which describes the proportion of people who die from a disease out of everyone formally diagnosed with the disease.
Simply speaking, R0 is a measure for transmissibility of the virus, while CFR is a measure for the fatality of the virus. In the case of the COVID-19 pandemic, different values have been reported for R0 and CFR, so they are not fully known. An important point to note is that the values of these parameters used to characterise COVID-19 in the Imperial and the Oxford models differ.
The Imperial model used an average R0 value of 2.4 (in other words, one person with COVID-19 will spread it to an average of 2.4 other people), but revised it to closer to 3 in the last few days. The Oxford model, on the other hand, uses R0 value of either 2.25 or 2.75 for different scenarios. The fact that they used different datasets to calibrate their models is maybe the reason they are using different R0 values – but I don’t know for sure.
In terms of fatalities, the Imperial model uses infection fatality rate (IFR) – not CFR. IFR is closely related to CFR but includes asymptomatic and undiagnosed cases, the total proportion of people who die out of everyone who has virus.
The Imperial model uses separate values for the IFR across different age groups with a mean value of 0.9% and range between 0.002% in those under ten years old and 9.3% in people over the age of 80. In contrast, the Oxford model uses a much lower CFR value of 0.14%. Using different values for COVID-19 infectiousness (R0) and fatality (CFR) will inevitably generate different results.
In terms of questions posed, the Imperial model asks: “Will mitigation or suppression strategies change the epidemic curve of covid-19?” And it answers: “Optimal mitigation policies … might reduce peak healthcare demand by 2/3 and deaths by half”.
The Oxford model asks: “Has COVID-19 already spread across a proportion of the population?” And the answer is that “ongoing epidemics in the UK and Italy started at least a month before the first reported death and have already led to the accumulation of significant levels of herd immunity in both countries”.
Other parts of the jigsaw
Both models have answered the questions they posed, with both answers important parts of the jigsaw of halting the spread of COVID-19. But it is now important to find the other parts of that jigsaw. The social-distancing mitigation strategy that Imperial suggests will be effective in “flattening the epidemic curve”, will inevitably reduce the COVID-19 transmission by simply reducing the number of contacts with possible infections.
The epidemic curve
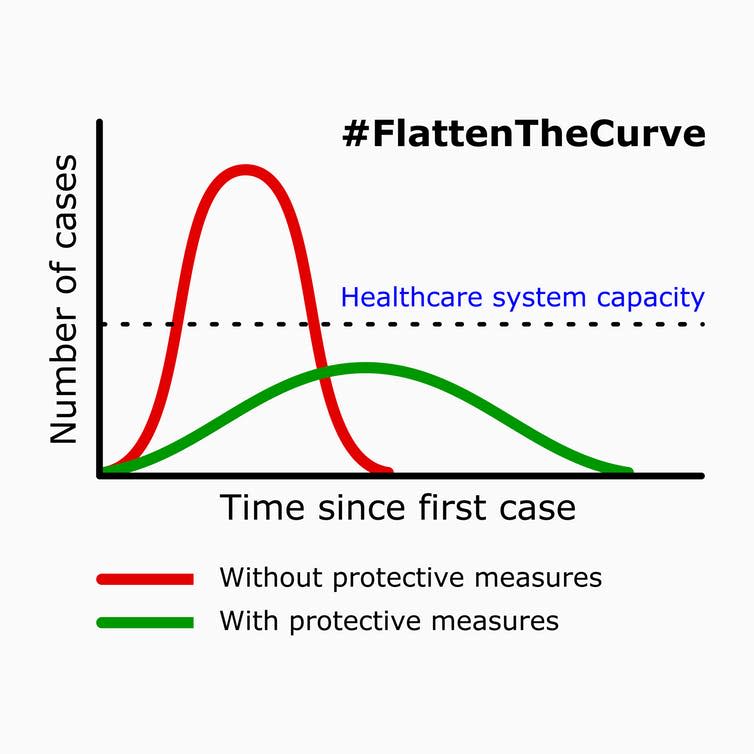
An important follow-up question is: when the restrictions are lifted, will the flattened curve rise again? Is the suppression strategy possibly an intermediate solution?
A couple of days ago, a study led by the Harvard T.H. Chan School of Public Health seems to suggest that intermittent and staggered social distancing measures “would save more lives than a one-and-done strategy and avoid overwhelming hospitals while allowing immunity to build in the population”.
Another independent crucial part of the jigsaw is whether there have been many asymptomatic COVID-19 cases, or whether the reported symptomatic cases make up most of the cases.
In the case of Sars, the number of asymptomatic or mildly symptomatic people after infection was quite low, so it was easier to isolate and contact trace the infected cases. We don’t yet have enough information whether this is the case with COVID-19. So possibly combining the strategies suggested by the Oxford and the Imperial models, that is, large-scale antibody testing within the current mitigating strategy may be the way forward.
Instead of focusing on which model is correct, we should accept that one model cannot answer it all. We need more models that answer complementary subquestions that can piece together the jigsaw and halt COVID-19 spread.
I am currently working on three different models exploring different preparedness measures for pandemic control and trying to quantify the proportion of asymptomatic and symptomatic infections emerging from COVID-19. Let’s hope we get some answers soon.
This article is republished from The Conversation under a Creative Commons license. Read the original article.

Jasmina Panovska-Griffiths has in the past received funding from the National Institute for Health Research, the UK Department of Health and Social Care, the World Bank and The Bill and Melinda Gates Foundation. The views expressed are those of the author and not necessarily those of these funders. The funders had no role in this study.

